CS & Programming
Computer Science Theory
This course is offered by Khan Academy. It is divided into three units.
UNIT 1: Algorithms
Automate the Boring Stuff With Python Programming
This course is taught by Al Sweigart on Udemy.
This course is offered by Khan Academy. It is divided into three units.
This course is taught by Al Sweigart on Udemy.
It has three parts:
Unit 1, is subdivided into these parts:
Unit 1, is subdivided into these parts:
In computer science, an algorithm is a set of setups for a computer to accomplish a task.
Algorithm are reason why there is a science in a computer science.
Examples:
Computer scientists have written an algorithm for a checker game, where the computer never lose.
Sometimes we need the algorithm to give us efficient but not necessarily the 100% accurate answer. For example, a truck needs to find a route between two locations, algorithm may take a lot of time to calculate the correct and the most efficient route. We will be okay for the program to calculate the good but maybe not the best route in the matter of seconds.
Computer Scientists use Asymptotic Analysis to find out the efficiency of an algorithm.
Asymptotic analysis is a method used in mathematical analysis and computer science to describe the limiting behavior of functions, particularly focusing on the performance of algorithms. It helps in understanding how an algorithm’s resource requirements, such as time and space, grow as the input size increases.
If we have to guess the number between 1 and 15, how and every time we guess, we are told, if our guessed number is lower or higher the actual number.
How to approach?
We will start from either 1 to keep increasing one digit until we reach the correct number, or start from 15 and keep decreasing 1 until the guess is right.
The method we use here is called a linear search.
Linear search, also known as sequential search, is a simple searching algorithm used to find an element within a list. It sequentially checks each element of the list until it finds a match or reaches the end of the list.
— Wikipedia
This is the inefficient way of finding the right number. If computer has selection 15, we will need to 15 guesses to reach the correct digit. If we are lucky and computer has selected 1, we can reach it in a single guess.
Another approach we can use is by taking average before each. First guess will be 8, if the guess is lower, we can eliminate all the numbers before 8, if the guess is higher, we can eliminate all the numbers from 8 to 15 and so on.
This approach is called Halving method. And in computer terms, it’s called Binary Search.
Using this technique maximum number of guesses needed can be found:
$$ \text{Maximum number of guesses} = \log_{2}(n) $$
Where n = Maximum Possible Guess
Binary search is a fast search algorithm used in computer science to find a specific element in a sorted array. It works on the principle of divide and conquer, reducing the search space by half with each step. The algorithm starts by comparing the target value with the middle element of the array. If the target value matches the middle element, the search is complete. If the target value is less or greater than the middle element, the search continues in the lower or upper half of the array, respectively. This process repeats until the target value is found, or the search space is exhausted.
— Wikipedia
Binary search is an algorithm for finding an item inside a sorted list. It finds it, by dividing the portion of the list in half repeatedly, which can possibly contain the item. The process goes on until the list is reduced to the last location.
Example
If we want to find a particular star in a Tycho-2 star catalog which contains information about the brightest 2,539,913 stars, in our galaxy.
Linear search would have to go through million of stars until the desired star is found. But through binary search algorithm, we can greatly reduce these guesses. For binary search to work, we need these start array to be sorted alphabetically.
Using this formula:
$$ \text{Maximum number of guesses} = \log_{2}(n) $$
where n = 2,539,913
$$ \text{Maximum number of guessess} \approx 22 $$
So, using binary search, the number of guesses are reduced to merely 22, to reach the desired name of the star.
When describing a computer algorithm to a fellow human, an incomplete description is often good enough. While describing a recipe, some details are intentionally left out, considering the reader/listener knows that anyway. For example, for a cake recipe, we don’t need to tell how to open a refrigerator to get ingredients out, or how to crack an egg. People might know to fill in the missing pieces, but the computer doesn’t. That’s why while giving instructions, we need to tell everything.
You need to provide answers to the following questions while writing an algorithm for a computer:
Here is the step-by-step guide of using binary search to play the guessing game:
min = 1 and max = n.max and min, rounded it, so that it’s an integer.min to be one larger than the guess.max to be one smaller than the guess.JavaScript and many other programming languages, already provide a way to find out if a given element is in the array or not. But to understand the logic behind it, we need to implement it ourselves.
var primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97];Let’s suppose we want to know if 67 is a prime number or not. If 67 is in the array, then it’s a prime.
We might also want to know how many primes are smaller than 67, we can do this by finding its index (position) in the array.
The position of an element in an array is known as its index.
Using binary search, $\text min = 2 , max = 97, guess = 41$
As $[ 41 < 67 ]$ so the elements less 41 would be discarded, and now
The next guess would be:
The binary search algorithm will stop here, as it has reached correct integer.
The binary search took only 2 guesses instead of 19 for linear search, to reach the right answer.
Here’s the pseudocode for binary search, modified for searching in an array. The inputs are the array, which we call array; the number n of elements in array; and target, the number being searched for. The output is the index in array of target:
min = 0 and max = n-1.guess as the average of max and min, rounded down (so that it is an integer).array[guess] equals target, then stop. You found it! Return guess.array[guess] < target, then set min = guess + 1.max = guess - 1.To turn pseudocode intro a program, we should create a function, as we’re writing a code that accepts an input and returns an output, and we want that code to be reusable for different inputs.
Then let’s go into the body of the function, and decide how to implement that. Step-6 says go back to step-2. That sound like a loop. Both for and while loops can be used here. But due to non-sequential guessing of the indexes, while loop will be more suitable.
min = 0 and max = n-1.max < min, then stop: target is not present in array. Return -1.guess as the average of max and min, rounded down (so that it is an integer).array[guess] equals target, then stop. You found it! Return guess.array[guess] < target, then set min = guess + 1.max = guess - 1.(If you don’t know JavaScript, you can skip the code challenges, or you can do the Intro to JS course and come back to them.)
Complete the doSearch function so that it implements a binary search, following the pseudo-code below (this pseudo-code was described in the previous article):
Once implemented, uncomment the Program.assertEqual() statement at the bottom to verify that the test assertion passes.
Linear search on an array of n elements might have to make as many as n guesses. We know, binary search need a lot less guesses. We also learned that as the length of an array increases, the efficiency of binary search goes up.
The idea is, when binary search makes an incorrect guess, number of reasonable guess left, are at least cut half. Binary search halves the size of the reasonable portion upon every incorrect guess.
Every time we double the size of an array, we require at most one more guess.
Let’s look at the general case of an array of length n, We can express the number of guesses, in the worst case, as “the number of time we can repeatedly halve, starting at n, until we get the value 1, plus one.” But this is inconvenient to write out.
Luckily, there’s a mathematical function that means the same thing as the base-2 logarithm of n. That’s the most often written as $\log_{2}(n)$.
| n | $\log_{2}(n)$ |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
| 512 | 9 |
| 1024 | 10 |
| 1,048,576 | 20 |
| 2,097,152 | 21 |
Graph of the same table:
Zooming in on smaller values of n:
The logarithm function grows very slowly. Logarithms are the inverse of exponentials, which grow very rapidly, so that if $\log_{2}(n) = x$, then $\ n = 2^{x}$. For example, $\ log_2 128 = 7$, we know that $\ 2^7 = 128$.
That makes it easy to calculate the runtime of a binary search algorithm on an $n$ that’s exactly a power of $2$. If $n$ is $128$, binary search will require at most $8 (log_2 128 + 1)$ guesses.
What if $n$ isn’t a power of $2$? In that case, we can look at the closest lower power of $2$. For an array whose length is 1000, the closest lower power of $2$ is $512$, which equals $2^9$. We can thus estimate that $log_2 1000$ is a number greater than $9$ and less than $10$, or use a calculator to see that its about $9.97$. Adding one to that yields about $10.97$. In the case of a decimal number, we round down to find the actual number of guesses. Therefore, for a 1000-element array, binary search would require at most 10 guesses.
For the Tycho-2 star catalog with 2,539,913 stars, the closest lower power of 2 is $2^{21}$ (which is 2,097,152), so we would need at most 22 guesses. Much better than linear search!
Compare $n$ vs $log_{2} {n}$ below:
So far, we analyzed linear search and binary search by counting the max number of guesses we need to make. But what we really want to know is how long these algorithms take. We are interested in time not just guesses. The running time of both include the time needed to make and check guesses.
The running time an algorithm depends on:
Let’s think more carefully about the running time. We can use a combination of two ideas.
We should say that running time of this algorithm grows as $n^2$, dropping the coefficient 6 and the remaining terms $100n+300$. It doesn’t really matter what coefficients we use; as long as the running time is $an^2+bn+c$, for some numbers a > 0, b, and c, there will always be a value of $n$ for which $an^2$ is greater than $bn+c$, and this difference increases as $n$ increases. For example, here’s a chart showing values of $0.6n^2$ and $1000n+3000$ so that we’ve reduced the coefficient of $n^2$ by a factor of 10 and increased the other two constants by a factor of 10:
The value of $n$ at which $0.6n^2$ becomes greater than $1000n+3000$ has increased, but there will always be such a crossover point, no matter what the constants.
By dropping the less significant terms and the constant coefficients, we can focus on the important part of an algorithm’s running time—its rate of growth—without getting mired in details that complicate our understanding. When we drop the constant coefficients and the less significant terms, we use asymptotic notation. We’ll see three forms of it: big-$\Theta$ (theta) notation, big-O notation, and big-$\Omega$ (omega) notation.
This course is offered by Harvard University, with David J. Malan as an instructor.
It is divided into following weekly modules:
This course is taught by Al Sweigart on Udemy. It has the following modules:
My notes are based on both the video course and the book Automate the Boring Stuff with Python by Al Sweigart.
| Coding Exercises | Python Automation Playground |
|---|
Everyone in their life, spent a lot of time on repetitive tasks, which can be automated through a simple script.
Automate the boring stuff with Python uses Python 3.
Being stuck while coding is a normal happening, but not asking for help isn’t.
When you go online to ask for help, make sure:
IDLE stands for Integrated Development and Learning Environment.
There are different programming text editors available:
Visual Studio Code
Sublime Text
PyCharm
Expressions = Values + Operators
In python, these expressions always evaluate to a single result. Arithmetic Operators are:
| Operator | Operation | Example | Evaluates to . . . |
|---|---|---|---|
| ** | Exponent | 2 ** 3 | 8 |
| % | Modulus/remainder | 22 % 8 | 6 |
| // | Integer division/floored quotient | 22 // 8 | 2 |
| / | Division | 22 / 8 | 2.75 |
| * | Multiplication | 3 * 5 | 15 |
| - | Subtraction | 5 - 2 | 3 |
| + | Addition | 2 + 2 | 4 |
+ symbol. (“Hello " + “World”)* operator. (3 * “Hello World!”)"Hello World" + "!" * 5Variable can store different values, like a box:
A too generic name given to a variable is a bad practice, which can create headache down the line while interacting with your code.
We can update the variable value by calling it down the line in the program:
>>> spam = 'Hello'
>>> spam
'Hello'
>>> spam = 'Goodbye'
>>> spam
'Goodbye'Just like the box, we can remove the old item with the new one.
You can name your variable anything, but Python does have some restrictions too:
Though Spam is a valid var, but it is a Python convention to start var name with a lowercase letter.
camelCase for variables can be used though Python PEP8 style guide instead recommends the use of underscores like this camel_case.
Though PEP8 guide itself says:
Consistency with the style guide is important. But most importantly: know when to be inconsistent—sometimes the style guide just doesn’t apply. When in doubt, use your best judgment.
#.print("Hello World!")
# Ask for their name
yourName = input("Type your name: ")
print("It is good to meet you, " + str(yourName))
print("Your name length is: " + str(len(yourName)))
# Ask for their age
print("What is your age?")
yourAge = input("Type your age: ")
print("You will be " + str(int(yourAge) + 1) + " in a year.")hello.py Evaluation steps look like this:
round(number, ndigits=None) FunctionReturn number rounded to ndigits precision after the decimal point. If ndigits is omitted or is None, it returns the nearest integer to its input.
>>> round(23)
23
>>> round(23.0)
23
>>> round(23.3)
23
>>> round(23.345)
23
>>> round(23.5)
24
>>> round(23.49)
23
>>> round(32.35, 1)
32.4
>>> round(32.355, 2)
32.35The behavior of round() for floats can be surprising: for example, round(2.675, 2) gives 2.67 instead of the expected 2.68. This is not a bug: it’s a result of the fact that most decimal fractions can’t be represented exactly as a float. See Floating-Point Arithmetic: Issues and Limitations for more information.
A flowchart starts at the start box, and you follow the arrow at the other boxes until you reach the end box. You take a different path depending on the conditions.
Based on how expression evaluate, a program can decide to skip instructions, repeat them, or choose one of several instructions to run. In fact, you almost never want your programs to start from the first line of ode and simply execute every line, straight to the end.
Flow control statements can decide which Python instructions to execute under which conditions.
These flow control statements directly correspond to the symbols in a flowchart.
In a flowchart, there is usually more than one way to go from the start to the end. The same is true for lines of code in a computer program. Flowcharts represent these branching points with diamonds, while the other steps are represented with rectangles. The starting and ending steps are represented with rounded rectangles.
Boolean Data Type has only to values True and False.
How to represent YES and NO values:
(Boolean is capitalized because the data type is named after mathematician George Boole)
➊ >>> spam = True
>>> spam
True
➋ >>> true
Traceback (most recent call last):
File "<pyshell#2>", line 1, in <module>
true
NameError: name 'true' is not defined
➌ >>> True = 2 + 2
SyntaxError: can't assign to keywordLike any other value, Boolean values are used in expressions and can be stored in variables ➊. If you don’t use the proper case ➋ or you try to use True and False for variable names ➌, Python will give you an error message.
They also called relational operators, compare two values and evaluate down to a single Boolean value.
| Operator | Meaning |
|---|---|
| == | Equal to |
| != | Not equal to |
| < | Less than |
| > | Greater than |
| <= | Less than or equal to |
| >= | Greater than or equal to |
== and != operators can actually work with values of any data type.>>> 'hello' == 'hello'
True
>>> 'hello' == 'Hello'
False
>>> 'dog' != 'cat'
True
>>> True == True
True
>>> True != False
True
>>> 42 == 42.0
True
➊ >>> 42 == '42'
FalseAn integer or floating point value will always be unequal to a string value. There 42 == '42'➊ evaluates to False because Python considers the integer 42 to be different from the string '42'.
The <, >, <=, and >= operators, on the other hand, work properly only with integer and floating-point values.
The three Boolean operators (and, or, and not) are used to compare Boolean values. Like comparison operators, they evaluate these expressions down to a Boolean value.
The and and or operators always take two Boolean values (or expressions), so they’re considered binary operators.
and Operator: It evaluates to True only if both Boolean values are True.
| Expression | Evaluates to… |
|---|---|
| True and True | True |
| True and False | False |
| False and True | False |
| False and False | False |
or Operator: It evaluates to True if one of the Boolean values is True.
| Expression | Evaluates to… |
|---|---|
| True or True | True |
| True or False | True |
| False or True | True |
| False or False | False |
not OperatorIt has only one Boolean value (or expression)
| Expression | Evaluates to… |
|---|---|
| not True | False |
| not False | True |
Since the comparison operators evaluate to Boolean values, you can use them in expressions with the Boolean operators.
>>> (4 < 5) and (5 < 6)
True
>>> (4 < 5) and (9 < 6)
False
>>> (1 == 2) or (2 == 2)
TrueYou can also use multiple Boolean operators in an expression, along with the comparison operators:
>>> 2 + 2 == 4 and not 2 + 2 == 5 and 2 * 2 == 2 + 2
TrueThe Boolean operators have an order of operations just like the math operators do. After any math and comparison operators evaluate, Python evaluates the not operators first, then the and operators, and then the or operators.
Flow control statements often start with a part called the condition and are always followed by a block of code called the clause.
The Boolean expressions you’ve seen so far could all be considered conditions, which are the same thing as expressions; condition is just a more specific name in the context of flow control statements.
Conditions always evaluate down to a Boolean value, True or False. A flow control statement decides what to do based on whether its condition is True or False, and almost every flow control statement uses a condition.
Lines of Python code can be grouped together in blocks.
There are 3 rules for block:
name = 'Mary'
password = 'swordfish'
if name == 'Mary':
➊ print('Hello, Mary')
if password == 'swordfish':
➋ print('Access granted.')
else:
➌ print('Wrong password.')You can view the execution of this program at https://autbor.com/blocks/. The first block of code ➊ starts at the line print(‘Hello, Mary’) and contains all the lines after it. Inside this block is another block ➋, which has only a single line in it: print(‘Access Granted.’). The third block ➌ is also one line long: print(‘Wrong password.’).
The statements represent the diamonds in the flowchart. They are the actual decisions your programs will make.
if StatementsIf this condition is true, execute the code in the clause. if statement, consists of the following:
if keywordif clause)else StatementsAn
ifclause can optionally be followed by an else statement. The else clause is executed only when the if statement’s condition is False.
An else statement doesn’t have a condition. In code, an else statement always consists of the following:
else keywordelse clause)elif StatementsWhile only one of the if or else clauses will execute, you may have a case where you want one of many possible clauses to execute.
The elif statement is an “else if” statement that always follows an if or another elif statement. It provides another condition that is checked only if all the previous conditions were False.
In code, an elif statement always consists of the following:
elif keywordTrue or False)elif clause)if name == 'Alice':
print('Hi, Alice.')
elif age < 12:
print('You are not Alice, kiddo.')The elif clause executes if age < 12 is True and name == 'Alice' is False. However, if both of the conditions are False, then both of the clauses are skipped. It is not guaranteed that at least one of the clauses will be executed. When there is a chain of elif statements, only one or none of the clauses will be executed. Once one of the statements’ conditions is found to be True, the rest of the elif clauses are automatically skipped.
name = 'Carol'
age = 3000
if name == 'Alice':
print('Hi, Alice.')
elif age < 12:
print('You are not Alice, kiddo.')
elif age > 2000:
print('Unlike you, Alice is not an undead, immortal vampire.')
elif age > 100:
print('You are not Alice, grannie.')vampire.py has 3 elif statements. If any of the three, is found True program execution will stop.elif statements is also important.else statement after the last elif statement. In that case, it is guaranteed that at least one (and only one) of the clauses will be executed. If the conditions in every if and elif statement are False, then the else clause is executed.For example, let’s re-create the Alice program to use if, elif, and else clauses.
age = 3000
if name == 'Alice':
print('Hi, Alice.')
elif age < 12:
print('You are not Alice, kiddo.')
else:
print('You are neither Alice nor a little kid.')When you use if, elif, and else statements together, remember these rules about how to order them to avoid bugs like the one in Figure 2.7. First, there is always exactly one if statement. Any elif statements you need should follow the if statement. Second, if you want to be sure that at least one clause is executed, close the structure with an else statement.
name = 'Carol'
age = 3000
if name == 'Alice':
print('Hi, Alice.')
elif age < 12:
print('You are not Alice, kiddo.')
elif age > 100:
print('You are not Alice, grannie.')
elif age > 2000:
print('Unlike you, Alice is not an undead, immortal vampire.')
Figure 2-7: The flowchart for the vampire2.py program. The X path will logically never happen, because if age were greater than 2000, it would have already been greater than 100.
The while statement always consists of the following:
while keywordTrue or False)while clause)You can see that a while statement looks similar to an if statement. The difference is in how they behave. At the end of an if clause, the program execution continues after the if statement. But at the end of a while clause, the program execution jumps back to the start of the while statement. The while clause is often called the while loop or just the loop.
The code with if statement:
spam = 0
if spam < 5:
print('Hello, world.')
spam = spam + 1The code with while statement:
spam = 0
while spam < 5:
print("Hello, world!")
spam = spam + 1Here is the code, which will keep asking your name until you literally type your name in the prompt:
name = ""
while name != 'your name':
print("Please type your name.")
name = input()
print("Thank you!")break StatementsIf the execution reaches a break statement, it immediately exits the while loop’s clause.
➊ while True:
print('Please type your name.')
➋ name = input()
➌ if name == 'your name':
➍ break
➎ print('Thank you!')The first line ➊ creates an infinite loop; it is a while loop whose condition is always True. (The expression True, after all, always evaluates down to the value True.) After the program execution enters this loop, it will exit the loop only when a break statement is executed. (An infinite loop that never exits is a common programming bug.)
Just like before, this program asks the user to enter your name ➋. Now, however, while the execution is still inside the while loop, an if statement checks ➌ whether name is equal to ‘your name’. If this condition is True, the break statement is run ➍, and the execution moves out of the loop to print(‘Thank you!’) ➎. Otherwise, the if statement’s clause that contains the break statement is skipped, which puts the execution at the end of the while loop. At this point, the program execution jumps back to the start of the while statement ➊ to recheck the condition.
continue Statementscontinue Statements are used inside loopscontinue statement, the program execution immediately jumps back to the start of the loop and re-evaluates the loop’s condition (This is also what happens when the execution reaches the end of the loop). while True:
print('Who are you?')
name = input()
➊ if name != 'Joe':
➋ continue
print('Hello, Joe. What is the password? (It is a fish.)')
➌ password = input()
if password == 'swordfish':
➍ break
➎ print('Access granted.')If the user enters any name besides Joe ➊, the continue statement ➋ causes the program execution to jump back to the start of the loop. When the program reevaluates the condition, the execution will always enter the loop, since the condition is simply the value True. Once the user makes it past that if statement, they are asked for a password ➌. If the password entered is swordfish, then the break statement ➍ is run, and the execution jumps out of the while loop to print Access granted ➎. Otherwise, the execution continues to the end of the while loop, where it then jumps back to the start of the loop.
The while loop keeps looping while its condition is True (which is the reason for its name), but what if you want to execute a block of code only a certain number of times? You can do this with a for loop statement and the range() function.
In code, a for statement looks something like for i in range(5): and includes the following:
for keywordin keywordrange() method with up to three integers passed to itfor clause)print("My name is")
for i in range(5):
print("Alex Five Times (" + str(i) + ")")The code in the for loop’s clause is run five times. The first time it is run, the variable i is set to 0. The print() call in the clause will print Jimmy Five Times (0). After Python finishes an iteration through all the code inside the for loop’s clause, the execution goes back to the top of the loop, and the for statement increments i by one. This is why range(5) results in five iterations through the clause, with i being set to 0, then 1, then 2, then 3, and then 4. The variable i will go up to, but will not include, the integer passed to range().
Counting the sums of all the numbers to 100 using both for and while loops:
# For Loop to Count the sums of numbers upto 100
sum = 0
for i in range(101):
sum = sum + i
# print(sum, i)
print("The sum of 100 using for loop is: ", sum)
# While Loop
#
sum = 0
i = 0
while i < 101:
sum = sum + i
i = i + 1
print("The sum of 100 using while loop is: ", sum)for is more efficient though while can also get the job done.Some functions can be called with multiple arguments separated by a comma, and range() is one of them. This lets you change the integer passed to range() to follow any sequence of integers, including starting at a number other than zero.
for i in range(12, 16):
print(i)The first argument will be where the for loop’s variable starts, and the second argument will be up to, but not including, the number to stop at.
12
13
14
15The range() function can also be called with three arguments. The first two arguments will be the start and stop values, and the third will be the step argument. The step is the amount that the variable is increased by after each iteration.
for i in range(0, 10, 2):
print(i)So calling range(0, 10, 2) will count from zero to eight by intervals of two.
0
2
4
6
8The range() function is flexible in the sequence of numbers it produces for for loops. You can even use a negative number for the step argument to make the for loop count down instead of up.
for i in range(5, -1, -1):
print(i)This for loop would have the following output:
5
4
3
2
1
0Running a for loop to print i with range(5, -1, -1) should print from five down to zero.
All Python programs can call a basic set of functions called built-in functions, including the print(), input(), and len() functions you’ve seen before.
Python also comes with a set of modules called the standard library.
Each module is a Python program that contains a related group of functions that can be embedded in your programs. For example, the
mathmodule has mathematics-related functions, therandommodule has random number-related functions, and so on.
Before you can use the functions in a module, you must import the module with an import statement. In code, an import statement consists of the following:
import keywordimport random
for i in range(5):
print(random.randint(1, 10))Since randint() is in the random module, you must first type random. in front of the function name to tell Python to look for this function inside the random module.
from import StatementsAn alternative form of the import statement is composed of the from keyword, followed by the module name, the import keyword, and a star; for example, from random import *.
With this form of import statement, calls to functions in random will not need the random. prefix. However, using the full name makes for more readable code, so it is better to use the import random form of the statement.
sys.exit() functionPrograms always terminate if the program execution reaches the bottom of the instructions. However, you can cause the program to terminate, or exit, before the last instruction by calling the sys.exit() function.
Since this function is in the sys module, you have to import sys before you can use it.
import sys
while True:
print('Type exit to quit.')
response = input()
if response == 'exit':
sys.exit()
print('You typed ' + "'" + response + "'" + '.')Run this program in IDLE. This program has an infinite loop with no break statement inside. The only way this program will end is if the execution reaches the sys.exit() call. When response is equal to exit, the line containing the sys.exit() call is executed. Since the response variable is set by the input() function, the user must enter exit in order to stop the program.
We have a pseudocode like this:
I am thinking of a number between 1 and 20.
Take a guess.
10
Your guess is too low.
Take a guess.
15
Your guess is too low.
Take a guess.
17
Your guess is too high.
Take a guess.
16
Good job! You guessed my number in 4 guesses!I have implemented this code as:
from random import randint
secretNumber = randint(1, 20)
# print(secretNumber) # Debuging purposes only
print("I am thinking of a number between 1 and 20.")
guess = ''
numberOfGuesses = 0
while guess != secretNumber:
guess = int(input("Take a Guess: "))
numberOfGuesses = numberOfGuesses + 1
if guess < secretNumber:
print("Your Guess is too low.")
elif guess > secretNumber:
print("Your Guess is too high")
print("Good job! You guessed my number in " +
str(numberOfGuesses) + " guesses!")We have the Pseudocode for the program:
ROCK, PAPER, SCISSORS
0 Wins, 0 Losses, 0 Ties
Enter your move: (r)ock (p)aper (s)cissors or (q)uit
p
PAPER versus...
PAPER
It is a tie!
0 Wins, 1 Losses, 1 Ties
Enter your move: (r)ock (p)aper (s)cissors or (q)uit
s
SCISSORS versus...
PAPER
You win!
1 Wins, 1 Losses, 1 Ties
Enter your move: (r)ock (p)aper (s)cissors or (q)uit
qThat’s how I implemented it:
##########################################
######## RPS GAME VERSION 5.0 ##########
##########################################
import random
import sys
# Print to the Screen Once
print("ROCK, PAPER, SCISSORS")
# Counting Streaks
wins = 0
losses = 0
ties = 0
while True:
# Print to the Screen
print("Enter your move: (r)ock (p)aper (s)cissors or (q)uit")
# User Input
userMove = input()
if userMove == "q":
print(f"Thank you for playing our Game!\n {
wins} Wins, {losses} losses, {ties} Ties")
sys.exit()
elif userMove != "r" and userMove != "p" and userMove != "s":
print("Illegal Guess, Try again.")
continue
elif userMove == "r":
userMove = "ROCK"
elif userMove == "p":
userMove = "PAPER"
elif userMove == "s":
userMove = "SCISSORS"
# System input
systemMove = random.randint(1, 3)
if systemMove == 1:
systemMove = "ROCK"
elif systemMove == 2:
systemMove = "PAPER"
elif systemMove == 3:
systemMove = "SCISSORS"
# Showing the Played Moves
print(f"{systemMove} vs. {userMove}")
# Game Logic
if systemMove == userMove:
print("It is a tie")
ties = ties + 1
elif (
(systemMove == "ROCK" and userMove == "PAPER")
or (systemMove == "SCISSORS" and userMove == "ROCK")
or (systemMove == "PAPER" and userMove == "SCISSORS")
):
print("You win!")
wins = wins + 1
elif (
(systemMove == "ROCK" and userMove == "SCISSORS")
or (systemMove == "PAPER" and userMove == "ROCK")
or (systemMove == "SCISSORS" and userMove == "PAPER")
):
print("Loser!")
losses = losses + 1abs() Function (Extras)The Python abs() function return the absolute value. The absolute value of any number is always positive it removes the negative sign of a number in Python.
>>> abs(-10)
10
>>> abs(-0.50)
0.5
>>> abs(-32.40)
32.4Python provides several built-in functions like print(), input() and len(), but you can also write your own functions.
A function is like a mini-program within a program.
➊ def hello():
➋ print('Howdy!')
print('Howdy!!!')
print('Hello there.')
➌ hello()
hello()
hello()The first line is a def statement ➊, which defines a function named hello(). The code in the block that follows the def statement ➋ is the body of the function. This code is executed when the function is called, not when the function is first defined.
The hello() lines after the function ➌ are function calls. In code, a function call is just the function’s name followed by parentheses, possibly with some number of arguments in between the parentheses.
A major purpose of functions is to group code that gets executed multiple times. Without a function defined, you would have to copy and paste this code each time, and the program would look like this:
print('Howdy!')
print('Howdy!!!')
print('Hello there.')
print('Howdy!')
print('Howdy!!!')
print('Hello there.')
print('Howdy!')
print('Howdy!!!')
print('Hello there.')def Statements with parametersprint() or len() function, are called arguments. They are typed between parentheses.➊ def hello(name):
➋ print('Hello, ' + name)
➌ hello('Alice')
hello('Bob')The definition of the hello() function in this program has a parameter called name ➊. Parameters are variables that contain arguments. When a function is called with arguments, the arguments are stored in the parameters. The first time the hello() function is called, it is passed the argument 'Alice' ➌. The program execution enters the function, and the parameter name is automatically set to 'Alice', which is what gets printed by the print() statement ➋.
print(name) after hello('Bob') in the previous program, the program would give a NameError because there is no variable named name.The terms define, call, pass, argument, and parameter can be confusing. Let’s look at a code example to review these terms:
➊ def sayHello(name):
print('Hello, ' + name)
➋ sayHello('Al')To define a function is to create it, just like an assignment statement like spam = 42 creates the spam variable. The def statement defines the sayHello() function ➊.
The sayHello('Al') line ➋ calls the now-created function, sending the execution to the top of the function’s code. This function call is also known as passing the string value 'Al' to the function.
A value being passed to a function in a function call is an argument. The argument 'Al' is assigned to a local variable named name. Variables that have arguments assigned to them are parameters.
It’s easy to mix up these terms, but keeping them straight will ensure that you know precisely what the text in this chapter means.
return StatementsCalling a len() function with an argument such as 'hello, will evaluate to the integer value 5, which is the length of the string passed.
The value that a function call evaluates to is called return value of the function.
While writing a function, return value should be used with return statement.
A return statement has:
return keywordWhen an expression is used with a return statement, the return value is what this expression evaluates to.
None ValueIn Python, there is a value called None, which represents the absence of a value(a placeholder). The None value is the only value of the NoneType data type.
null, nil, or undefined.True and False values, None must be typed with a capital N.None is used is as the return value of print().The print() function displays text on the screen, but it doesn’t need to return anything in the same way len() or input() does. But since all function calls need to evaluate to a return value, print() returns None. To see this in action, enter the following into the interactive shell:
>>> spam = print('Hello!')
Hello!
>>> None == spam
TrueBehind the scenes, Python adds return None to the end of any function definition with no return statement. This is similar to how a while or for loop implicitly ends with a continue statement. Also, if you use a return statement without a value (that is, just the return keyword by itself), then None is returned.
print() FunctionKeyword arguments are often used for optional parameters. For example, the print() function has the optional parameters end and sep to specify what should be printed at the end of its arguments and between its arguments (separating them), respectively.
By default, two successive print statements would print their arguments on a separate line, but we can change this behavior with keyword arguments:
print('Hello', end=' ')
print('World')When different strings are concatenated, we can use:
print('Hello!' + 'World', sep=':')Imagine that you have a meandering conversation with someone. You talk about your friend Alice, which then reminds you of a story about your coworker Bob, but first you have to explain something about your cousin Carol. You finish you story about Carol and go back to talking about Bob, and when you finish your story about Bob, you go back to talking about Alice. But then you are reminded about your brother David, so you tell a story about him, and then get back to finishing your original story about Alice. Your conversation followed a stack-like structure, like in Figure 3-1. The conversation is stack-like because the current topic is always at the top of the stack.
Similar to our meandering conversation, calling a function doesn’t send the execution on a one-way trip to the top of a function. Python will remember which line of code called the function so that the execution can return there when it encounters a return statement. If that original function called other functions, the execution would return to those function calls first, before returning from the original function call.
def a():
print('a() starts')
b()
d()
print('a() returns')
def b():
print('b() starts')
c()
print('b() returns')
def c():
print('c() starts')
print('c() returns')
def d():
print('d() starts')
print('d() returns')
a()Output of this program looks like this:
a() starts
b() starts
c() starts
c() returns
b() returns
d() starts
d() returns
a() returnsThe call stack is how Python remembers where to return the execution after each function call.
The call stack isn’t stored in a variable in your program; rather, Python handles it behind the scenes.
When your program calls a function, Python creates a frame object on the top of the call stack. Frame objects store the line number of the original function call so that Python can remember where to return. If another function call is made, Python puts another frame object on the call stack above the other one.
When a function call returns, Python removes a frame object from the top of the stack and moves the execution to the line number stored in it. Note that frame objects are always added and removed from the top of the stack and not from any other place.
The top of the call stack is which function the execution is currently in. When the call stack is empty, the execution is on a line outside of all functions.
Parameters and variables that are assigned in a called function are said to exit in that function’s local scope.
Variables that are assigned outside all functions are said to exist in the global scope.
Scope matter because:
def spam():
print(eggs)
eggs = 42
spam()
print(eggs)Using global variables in small programs is fine, it’s a bad habit to rely on global variables as your programs get larger and larger.
To modify a global variable from within a function, we can use a global statement.
If you have a line such as global eggs at the top of a function, it tells Python, “In this function, eggs refers to the global variable, so don’t create a local variable with this name.”
def spam():
➊ global eggs
➋ eggs = 'spam'
eggs = 'global'
spam()
print(eggs)Above code evaluates to:
spamBecause eggs is declared global at the top of spam() ➊, when eggs is set to 'spam' ➋, this assignment is done to the globally scoped eggs. No local eggs variable is created.
There are four rules to tell whether a variable is in a local scope or global scope:
global statement for that variable in a function, it is a global variable.Getting an error or exception in Python program, without any exception handling means entire program will crash.
In real world, this is not the desired behavior, and we want our program to detect errors, handle them, and then continue to run.
|
|
When the program is run we will get ZeroDivisonError at line 6.
You can put the previous divide-by-zero code in a try clause and have an except clause contain code to handle what happens when this error occurs.
|
|
When code in a try clause causes an error, the program execution immediately moves to the code in the except clause. After running that code, the execution continues as normal.
This program will create a back-and-forth, zigzag pattern until the user stops it by pressing the Mu editor’s Stop button or by pressing CTRL-C. When you run this program, the output will look something like this:
********
********
********
********
********
********
********
********
********This is how I implemented:
|
|
Here is Al’s implementation
Write a function named collatz() that has one parameter named number. If number is even, then collatz() should print number // 2 and return this value. If number is odd, then collatz() should print and return 3 * number + 1.
Then write a program that lets the user type in an integer and that keeps calling collatz() on that number until the function returns the value 1. (Amazingly enough, this sequence actually works for any integer—sooner or later, using this sequence, you’ll arrive at 1! Even mathematicians aren’t sure why. Your program is exploring what’s called the Collatz sequence, sometimes called “the simplest impossible math problem.”)
Remember to convert the return value from input() to an integer with the int() function; otherwise, it will be a string value.
Hint: An integer number is even if number % 2 == 0, and it’s odd if number % 2 == 1.
The output of this program could look something like this:
Enter number:
3
10
5
16
8
4
2
1
|
|
The output we need:
Hello, What is your name?
Al
Well, Al, I am thinking of a number between 1 and 20.
Take a guess.
10
Your guess is too low.
Take a guess
5
Your guess is too high.
Take a guess.
6
Good job, Al! You guessed my number in 5 guesses!
|
|
In this course we were taught about string concatenation using + operator. But that is cumbersome, and we need to convert non-strings values to strings values for concatenation to work.
In python 3.6, F-strings were introduced, that makes the strings concatenation a lot easier.
print(f"This is an example of {strings} concatenation."){} We can put our variable name, which will be automatically converted into string type. As you can see, this approach is much more cleaner.
Let’s take everything we learned so far, write a guess game which has the following qualities:
sys.exit() module or pressing q(uit) button on their keyboard.title() method, convert a string into title case, where the first letter of each word is capitalized, and the rest are in lowercase.An extra feature which I want to implement is telling the player, how many guesses they will get. As taught in Algorithm: Binary Search course, offered by Khan Academy. We can calculate max number of guesses using this formula:
$$ \text{Maximum number of guesses} = \log_{2}(n) \ $$
For guess between (1, 20), the n = 20:
$$ \text{Maximum number of guesses} = \log_{2}(20) $$
$$ \text{Maximum number of guessess} \approx 5 $$
Here is the extended version, I might have gone a bit over the board.
|
|
0, not 1.-1 refers to the last item, -2 refers to the second to last item, and so on.A list is a value that contains multiple values in an ordered sequence. The term list value refers to the list itself (which is a value that can be stored in a variable or passed to a function like any other value), not the values inside the list value.
>>> [1, 2, 3]
[1, 2, 3]
>>> ['cat', 'bat', 'rat', 'elephant']
['cat', 'bat', 'rat', 'elephant']
>>> ['hello', 3.1415, True, None, 42]
['hello', 3.1415, True, None, 42]
➊ >>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam
['cat', 'bat', 'rat', 'elephant']The spam variable ➊ is still assigned only one value: the list value. But the list value itself contains other values. The value [] is an empty list that contains no values, similar to '', the empty string.
Lists can also contain other list values. The values in these lists of lists can be accessed using multiple indexes, like so:
>>> spam = [['cat', 'bat'], [10, 20, 30, 40, 50]]
>>> spam[0]
['cat', 'bat']
>>> spam[0][1]
'bat'
>>> spam[1][4]
50The first index dictates which list value to use, and the second indicates the value within the list value.
The integer value -1 refers to the last index in a list, the value -2 refers to the second-to-last index in a list, and so on.
>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam[-1]
'elephant'
>>> spam[-3]
'bat'
>>> 'The ' + spam[-1] + ' is afraid of the ' + spam[-3] + '.'
'The elephant is afraid of the bat.'Just as an index can get a single value from a list, a slice can get several values from a list, in the form of a new list. A slice goes up to, but will not include, the value at the second index.
spam[2] is a list with an index (one integer).spam[1:4] is a list with a slice (two integers)>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam[0:4]
['cat', 'bat', 'rat', 'elephant']
>>> spam[1:3]
['bat', 'rat']
>>> spam[0:-1]
['cat', 'bat', 'rat']As a shortcut, you can leave out one or both of the indexes on either side of the colon in the slice. Leaving out the first index is the same as using 0, or the beginning of the list. Leaving out the second index is the same as using the length of the list, which will slice to the end of the list. Enter the following into the interactive shell:
>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam[:2]
['cat', 'bat']
>>> spam[1:]
['bat', 'rat', 'elephant']
>>> spam[:]
['cat', 'bat', 'rat', 'elephant']len() FunctionThe len() function will return the number of values that are in a list value passed to it, just like it can count the number of characters in a string value.
>>> spam = ['cat', 'dog', 'moose']
>>> len(spam)
3>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam[1] = 'aardvark'
>>> spam
['cat', 'aardvark', 'rat', 'elephant']
>>> spam[2] = spam[1]
>>> spam
['cat', 'aardvark', 'aardvark', 'elephant']
>>> spam[-1] = 12345
>>> spam
['cat', 'aardvark', 'aardvark', 12345]>>> [1, 2, 3] + ['A', 'B', 'C']
[1, 2, 3, 'A', 'B', 'C']
>>> ['X', 'Y', 'Z'] * 3
['X', 'Y', 'Z', 'X', 'Y', 'Z', 'X', 'Y', 'Z']
>>> spam = [1, 2, 3]
>>> spam = spam + ['A', 'B', 'C']
>>> spam
[1, 2, 3, 'A', 'B', 'C']del StatementsThe del statement will delete values at an index in a list. All the values in the list after the deleted value will be moved up one index.
>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> del spam[2]
>>> spam
['cat', 'bat', 'elephant']
>>> del spam[2]
>>> spam
['cat', 'bat']The del statement can also be used on a simple variable to delete it, as if it were an “un-assignment” statement. If you try to use the variable after deleting it, you will get a NameError error because the variable no longer exists. In practice, you almost never need to delete simple variables. The del statement is mostly used to delete values from lists.
Let’s look at the example of bad code using a lot of variables to store a group of similar values:
print('Enter the name of cat 1:')
catName1 = input()
print('Enter the name of cat 2:')
catName2 = input()
print('Enter the name of cat 3:')
catName3 = input()
print('Enter the name of cat 4:')
catName4 = input()
print('Enter the name of cat 5:')
catName5 = input()
print('Enter the name of cat 6:')
catName6 = input()
print('The cat names are:')
print(catName1 + ' ' + catName2 + ' ' + catName3 + ' ' + catName4 + ' ' +
catName5 + ' ' + catName6)Improved version:
catName = []
while True:
print(f"Enter your cat name: {
len(catName) + 1} (Or Enter nothing to stop.)")
name = input()
if name == '':
break
catName = catName + [name]
print("The cat names are: ")
for name in catName:
print(f" {name}")for Loops with Lists, Multiple Assignment, and Augmented Operatorsrange() function returns a list-like value, which can be passed to the list() function if you need an actual list value.+= are used as shortcuts.for Loops with Listsfor Loops execute a block of code a certain number of times. Technically, a for loop repeats the code block once for each item in a list value.
#input
for i in range(4):
print(i)
#output
0
1
2
3This is because the return value from range(4) is a sequence value that Python considers similar to [0,1,2,3] (Sequence Data Types).
The following program has same output as the previous one:
for i in [0, 1, 2, 3]:
print(i)A common Python technique is to use range(len(someList)) with a for loop to iterate over the indexes of a list.
supplies = ['pens', 'staplers', 'printers', 'binders']
for i in range(len(supplies)):
print(f"Index of {i} in supplies is: {supplies[i]}")
Index 0 in supplies is: pens
Index 1 in supplies is: staplers
Index 2 in supplies is: printers
Index 3 in supplies is: bindersin and not in OperatorsThe in and not in operators are used to determine whether a value is or isn’t in a list.
>>> 'howdy' in ['hello', 'hi', 'howdy', 'heyas']
True
>>> spam = ['hello', 'hi', 'howdy', 'heyas']
>>> 'cat' in spam
False
>>> 'howdy' not in spam
False
>>> 'cat' not in spam
TrueProgram: Write a program that lets the user type in a pet name and then checks to see whether the name is in a list of pets.
The multiple assignment trick (technically called tuple unpacking) is a shortcut that lets you assign multiple variables with the values in a list in one line of code. So instead of doing this:
>>> cat = ['fat', 'gray', 'loud']
>>> size = cat[0]
>>> color = cat[1]
>>> disposition = cat[2]you could write code like this:
>>> cat = ['fat', 'gray', 'loud']
>>> size, color, disposition = catThe number of variables and the length of the list must be exactly equal, or Python will give you a ValueError.
enumerate() Function with ListsInstead of using range(len(someList)) technique, enumerate() returns both list item, and its index, when called upon a list.
>>> supplies = ['pens', 'staplers', 'flamethrowers', 'binders']
>>> for index, item in enumerate(supplies):
... print('Index ' + str(index) + ' in supplies is: ' + item)
Index 0 in supplies is: pens
Index 1 in supplies is: staplers
Index 2 in supplies is: flamethrowers
Index 3 in supplies is: bindersThe enumerate() function is useful if you need both the item and the item’s index in the loop’s block.
random.choice() and random.shuffle() Functions with ListsThe random module has a couple of functions that accept lists for arguments. The random.choice() function will return a randomly selected item from the list.
>>> import random
>>> pets = ['Dog', 'Cat', 'Moose']
>>> random.choice(pets)
'Dog'
>>> random.choice(pets)
'Cat'
>>> random.choice(pets)
'Cat'Consider random.choice(someList) to be a shorter form of someList[random.randint(0, len(someList) - 1].
The random.shuffle() function will reorder the items in the list, without need to return a new list.
>>> import random
>>> people = ['Alice', 'Bob', 'Carol', 'David']
>>> random.shuffle(people)
>>> people
['Carol', 'David', 'Alice', 'Bob']
>>> random.shuffle(people)
>>> people
['Alice', 'David', 'Bob', 'Carol']| Augmented assignment statement | Equivalent assignment statement |
|---|---|
| spam += 1 | spam = spam + 1 |
| spam -= 1 | spam = spam - 1 |
| spam *= 1 | spam = spam * 1 |
| spam /= 1 | spam = spam / 1 |
| spam %= 1 | spam = spam % 1 |
The += operator can also do string and list concatenation, and the *= operator can do string and list replication.
>>> spam = 'Hello,'
>>> spam += ' world!'
>>> spam
'Hello world!'
>>> bacon = ['Zophie']
>>> bacon *= 3
>>> bacon
['Zophie', 'Zophie', 'Zophie']index() list method returns the index of an item in the list.append() list method adds a value to the end of the list.insert() list method adds a value anywhere inside a list.remove() list method removes an item, specified by the value, from a list.sort() list method sorts the items in a list.sort() method’s reverse=True keyword argument can sort in reverse order.append() and insert() methods are list methods and can be only called on list values, not on other values such as strings or integers.str or inte will give the error AttributeError.Each data type has its own set of methods. This list data type, for example, has several useful methods for finding, adding, removing, and other manipulating values in a list.
index() Method>>> spam = ['hello', 'hi', 'howdy', 'heyas']
>>> spam.index('hello')
0
>>> spam.index('heyas')
3
>>> spam.index('howdy howdy howdy')
Traceback (most recent call last):
File "<pyshell#31>", line 1, in <module>
spam.index('howdy howdy howdy')
ValueError: 'howdy howdy howdy' is not in listappend() and insert() Methods>>> spam = ['cat', 'dog', 'bat']
>>> spam.append('moose')
>>> spam
['cat', 'dog', 'bat', 'moose']The append() methods adds item to the end of the list, insert() method can insert a value at any index in the list.
>>> spam = ['cat', 'dog', 'bat']
>>> spam.insert(1, 'chicken')
>>> spam
['cat', 'chicken', 'dog', 'bat']Notice that the code is spam.append('moose') and spam.insert(1, 'chicken'), not spam = spam.append('moose') and spam = spam.insert(1, 'chicken'). Neither append() nor insert() gives the new value of spam as its return value. (In fact, the return value of append() and insert() is None, so you definitely wouldn’t want to store this as the new variable value.) Rather, the list is modified in place. Modifying a list in place is covered in more detail later in Mutable and Immutable Data Types.
remove() Method>>> spam = ['cat', 'bat', 'rat', 'elephant']
>>> spam.remove('bat')
>>> spam
['cat', 'rat', 'elephant']ValueError error.del statement is good to use when you know the index of the value, you want to remove from the list.remove() method is useful when you know the value you want to remove from list.>>> spam = [2, 5, 3.14, 1, -7]
>>> spam.sort()
>>> spam
[-7, 1, 2, 3.14, 5]
>>> spam = ['ants', 'cats', 'dogs', 'badgers', 'elephants']
>>> spam.sort()
>>> spam
['ants', 'badgers', 'cats', 'dogs', 'elephants']You can also pass True for the reverse keyword argument to have sort() sort the values in reverse order.
>>> spam.sort(reverse=True)
>>> spam
['elephants', 'dogs', 'cats', 'badgers', 'ants']sort() method sorts the list in place, don’t try to capture the return value writing code like spam = spam.sort().sort() uses ASCII-betical order rather than actual alphabetical order for sorting strings. This means uppercase letters come before lowercase letters.>>> spam = ['Alice', 'ants', 'Bob', 'badgers', 'Carol', 'cats']
>>> spam.sort()
>>> spam
['Alice', 'Bob', 'Carol', 'ants', 'badgers', 'cats']For regular alphabetical order:
>>> spam = ['a', 'z', 'A', 'Z']
>>> spam.sort(key=str.lower)
>>> spam
['a', 'A', 'z', 'Z']reverse() Methodsort() list method, reverse() doesn’t return a list.>>> spam = ['cat', 'dog', 'moose']
>>> spam.reverse()
>>> spam
['moose', 'dog', 'cat']\ line continuation character can be used to stretch Python instructions across multiple lines.Lists aren’t the only data types that represent ordered sequences of values.
range(), and tuples.len(), and with in and not in operators.>>> name = 'Zophie'
>>> name[0]
'Z'
>>> name[-2]
'i'
>>> name[0:4]
'Zoph'
>>> 'Zo' in name
True
>>> 'z' in name
False
>>> 'p' not in name
False
>>> for i in name:
... print('* * * ' + i + ' * * *')
* * * Z * * *
* * * o * * *
* * * p * * *
* * * h * * *
* * * i * * *
* * * e * * *A list value:
A string value is:
Trying to reassign a single character in a string results in a TypeError error:
>>> name = 'Zophie a cat'
>>> name[7] = 'the'
Traceback (most recent call last):
File "<pyshell#50>", line 1, in <module>
name[7] = 'the'
TypeError: 'str' object does not support item assignmentThe proper way to “mutate” a string is to use slicing and concatenation to build a new string by copying from parts of the old string.
>>> name = 'Zophie a cat'
>>> newName = name[0:7] + 'the' + name[8:12]
>>> name
'Zophie a cat'
>>> newName
'Zophie the cat'Although a list value is mutable:
>>> eggs = [1, 2, 3]
>>> eggs = [4, 5, 6]
>>> eggs
[4, 5, 6]The list value in eggs isn’t being changed here; rather, an entirely new and different list value [4, 5, 6] is overwriting the old list.
For actually modifying the list:
>>> eggs = [1, 2, 3]
>>> del eggs[2]
>>> del eggs[1]
>>> del eggs[0]
>>> eggs.append(4)
>>> eggs.append(5)
>>> eggs.append(6)
>>> eggs
[4, 5, 6]The tuple data type is almost identical to the list data type, except in two ways:
().>>> eggs = ('hello', 42, 0.5)
>>> eggs[0]
'hello'
>>> eggs[1:3]
(42, 0.5)
>>> len(eggs)
3If you have only one value in your tuple, you cna indicate this by placing a trailing comma after the value inside the parentheses. Otherwise, Python will think you’ve just typed a value inside regular parentheses.
>>> type(('hello',))
<class 'tuple'>
>>> type(('hello'))
<class 'str'>You can use tuples to convey to anyone reading your code that you don’t intend for that sequence of values to change. If you need an ordered sequence of values that never changes, use a tuple. A second benefit of using tuples instead of lists is that, because they are immutable, and their contents don’t change, Python can implement some optimizations.
list() and tuple() FunctionsJust like how str(42) will return '42', the string representation of the integer 42, the functions list() and tuple() will return list and tuple versions of the values passed to them:
>>> tuple(['cat', 'dog', 5])
('cat', 'dog', 5)
>>> list(('cat', 'dog', 5))
['cat', 'dog', 5]
>>> list('hello')
['h', 'e', 'l', 'l', 'o']Converting a tuple to a list is handy if you need a mutable version of a tuple value.
As you’ve seen, variables “store” strings and integer values. However, this explanation is a simplification of what Python is actually doing. Technically, variables are storing references to the computer memory locations where the values are stored.
>>> spam = 42
>>> cheese = spam
>>> spam = 100
>>> spam
100
>>> cheese
42When you assign 42 to the spam variable, you are actually creating the 42 value in the computer’s memory and storing a reference to it in the spam variable. When you copy the value in spam and assign it to the variable cheese, you are actually copying the reference. Both the spam and cheese variables refer to the 42 value in the computer’s memory. When you later change the value in spam to 100, you’re creating a new 100 value and storing a reference to it in spam. This doesn’t affect the value in cheese. Integers are immutable values that don’t change; changing the spam variable is actually making it refer to a completely different value in memory.
But lists don’t work this way, because list values can change; that is, lists are mutable. Here is some code that will make this distinction easier to understand.
➊ >>> spam = [0, 1, 2, 3, 4, 5]
➋ >>> cheese = spam # The reference is being copied, not the list.
➌ >>> cheese[1] = 'Hello!' # This changes the list value.
>>> spam
[0, 'Hello!', 2, 3, 4, 5]
>>> cheese # The cheese variable refers to the same list.
[0, 'Hello!', 2, 3, 4, 5]This might look odd to you. The code touched only the cheese list, but it seems that both the cheese and spam lists have changed.
When you create the list ➊, you assign a reference to it in the spam variable. But the next line ➋ copies only the list reference in spam to cheese, not the list value itself. This means the values stored in spam and cheese now both refer to the same list. There is only one underlying list because the list itself was never actually copied. So when you modify the first element of cheese ➌, you are modifying the same list that spam refers to.
What happens when a list is assigned to the spam variable.
Then, the reference in spam is copied to cheese. Only a new reference was created and stored in cheese, not a new list. Note how both references refer to the same list.
When you alter the list that cheese refers to, the list that spam refers to is also changed, because both cheese and spam refer to the same list.
id() FunctionWhy the weird behavior with mutable lists in the previous section doesn’t happen with immutable values like integers or strings.
We can use Python’s id() function to understand this. All values in Python have a unique identity that can be obtained with the id() function.
> id('Howdy') # The returned number will be different on your machine.
139789342729024When Python runs id('Howdy'), it creates the 'Howdy' string in the computer’s memory. The numeric memory address where the string is stored is returned by the id() function. Python picks this address based on which memory bytes happen to be free on your computer at the time, so it’ll be different each time you run this code.
Like all strings, 'Howdy' is immutable and cannot be changed. If you “change” the string in a variable, a new string object is being made at a different place in memory, and the variable refers to this new string. For example, enter the following into the interactive shell and see how the identity of the string referred to by bacon changes:
>>> bacon = 'Hello'
>>> id(bacon)
139789339474704
>>> bacon += ' world!' # A new string is made from 'Hello' and ' world!'.
>>> id(bacon) # bacon now refers to a completely different string.
139789337326704However, lists can be modified because they are mutable objects. The append() method doesn’t create a new list object; it changes the existing list object. We call this modifying the object in-place.
>>> eggs = ['cat', 'dog'] # This creates a new list.
>>> id(eggs)
139789337916608
>>> eggs.append('moose') # append() modifies the list "in place".
>>> id(eggs) # eggs still refers to the same list as before.
139789337916608
>>> eggs = ['bat', 'rat', 'cow'] # This creates a new list, which has a new identity.
>>> id(eggs) # eggs now refers to a completely different list.
139789337915136References are particularly important for understanding how arguments get passed to functions. When a function is called, the values of the arguments are copied to the parameter variables. For lists (and dictionaries, which I’ll describe in the next chapter), this means a copy of the reference is used for the parameter.
def eggs(someParameter):
someParameter.append('Hello')
spam = [1, 2, 3]
eggs(spam)
print(spam)Notice that when eggs() is called, a return value is not used to assign a new value to spam. Instead, it modifies the list in place, directly. When run, this program produces the following output:
[1, 2, 3, 'Hello']Even though spam and someParameter contain separate references, they both refer to the same list. This is why the append('Hello') method call inside the function affects the list even after the function call has returned.
Keep this behavior in mind: forgetting that Python handles list and dictionary variables this way can lead to confusing bugs.
copy() and deepcopy() FunctionsAlthough passing around references is often the handiest way to deal with lists and dictionaries, if the function modifies the list or dictionary that is passed, you may not want these changes in the original list or dictionary value. For this, Python provides a module named copy that provides both the copy() and deepcopy() functions. The first of these, copy.copy(), can be used to make a duplicate copy of a mutable value like a list or dictionary, not just a copy of a reference.
>>> import copy
>>> spam = ['A', 'B', 'C', 'D']
>>> id(spam)
139789337916608
>>> cheese = copy.copy(spam)
>>> id(cheese) # cheese is a different list with different identity.
139789337915776
>>> cheese[1] = 42
>>> spam
['A', 'B', 'C', 'D']
>>> cheese
['A', 42, 'C', 'D']Now the spam and cheese variables refer to separate lists, which is why only the list in cheese is modified when you assign 42 at index 1.
If the list you need to copy contains lists, then use the copy.deepcopy() function instead of copy.copy() The deepcopy() function will these inner lists as well.
There are following project given in the book. Check their code at my GitHub.
Conway’s Game of Life is an example of cellular automata: a set of rules governing the behavior of a field made up of discrete cells. In practice, it creates a pretty animation to look at. You can draw out each step on graph paper, using the squares as cells. A filled-in square will be “alive” and an empty square will be “dead.” If a living square has two or three living neighbors, it continues to live on the next step. If a dead square has exactly three living neighbors, it comes alive on the next step. Every other square dies or remains dead on the next step.
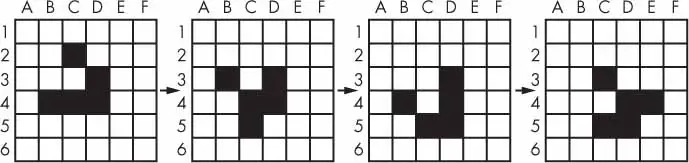
Four steps in a Conway’s Game of Life Simulation
Even though the rules are simple, there are many surprising behaviors that emerge. Patterns in Conway’s Game of Life can move, self-replicate, or even mimic CPUs. But at the foundation of all of this complex, advanced behavior is a rather simple program.
We can use a list of lists to represent the two-dimensional field. The inner list represents each column of squares and stores a '#' hash string for living squares and a ' ' space string for dead squares.
Say you have a list value like this:
spam = ['apples', 'bananas', 'tofu', 'cats']Write a function that takes a list value as an argument and returns a string with all the items separated by a comma and a space, with and inserted before the last item. For example, passing the previous spam list to the function would return 'apples, bananas, tofu, and cats'. But your function should be able to work with any list value passed to it. Be sure to test the case where an empty list [] is passed to your function.
For this exercise, we’ll try doing an experiment. If you flip a coin 100 times and write down an “H” for each heads and “T” for each tails, you’ll create a list that looks like “T T T T H H H H T T.” If you ask a human to make up 100 random coin flips, you’ll probably end up with alternating head-tail results like “H T H T H H T H T T,” which looks random (to humans), but isn’t mathematically random. A human will almost never write down a streak of six heads or six tails in a row, even though it is highly likely to happen in truly random coin flips. Humans are predictably bad at being random.
Write a program to find out how often a streak of six heads or a streak of six tails comes up in a randomly generated list of heads and tails. Your program breaks up the experiment into two parts: the first part generates a list of randomly selected ‘heads’ and ’tails’ values, and the second part checks if there is a streak in it. Put all of this code in a loop that repeats the experiment 10,000 times so we can find out what percentage of the coin flips contains a streak of six heads or tails in a row. As a hint, the function call random.randint(0, 1) will return a 0 value 50% of the time and a 1 value the other 50% of the time.
You can start with the following template:
import random
numberOfStreaks = 0
for experimentNumber in range(10000):
# Code that creates a list of 100 'heads' or 'tails' values.
# Code that checks if there is a streak of 6 heads or tails in a row.
print('Chance of streak: %s%%' % (numberOfStreaks / 100))Of course, this is only an estimate, but 10,000 is a decent sample size. Some knowledge of mathematics could give you the exact answer and save you the trouble of writing a program, but programmers are notoriously bad at math.
Say you have a list of lists where each value in the inner lists is a one-character string, like this:
grid = [['.', '.', '.', '.', '.', '.'],
['.', 'O', 'O', '.', '.', '.'],
['O', 'O', 'O', 'O', '.', '.'],
['O', 'O', 'O', 'O', 'O', '.'],
['.', 'O', 'O', 'O', 'O', 'O'],
['O', 'O', 'O', 'O', 'O', '.'],
['O', 'O', 'O', 'O', '.', '.'],
['.', 'O', 'O', '.', '.', '.'],
['.', '.', '.', '.', '.', '.']]Think of grid[x][y] as being the character at the x- and y-coordinates of a “picture” drawn with text characters. The (0, 0) origin is in the upper-left corner, the x-coordinates increase going right, and the y-coordinates increase going down.
Copy the previous grid value, and write code that uses it to print the image.
..OO.OO..
.OOOOOOO.
.OOOOOOO.
..OOOOO..
...OOO...
....O....Hint: You will need to use a loop in a loop in order to print grid[0][0], then grid[1][0], then grid[2][0], and so on, up to grid[8][0]. This will finish the first row, so then print a newline. Then your program should print grid[0][1], then grid[1][1], then grid[2][1], and so on. The last thing your program will print is grid[8][5].
Also, remember to pass the end keyword argument to print() if you don’t want a newline printed automatically after each print() call.