Binary Search
Binary search is an algorithm for finding an item inside a sorted list. It finds it, by dividing the portion of the list in half repeatedly, which can possibly contain the item. The process goes on until the list is reduced to the last location.
Example
If we want to find a particular star in a Tycho-2 star catalog which contains information about the brightest 2,539,913 stars, in our galaxy.
Linear search would have to go through million of stars until the desired star is found. But through binary search algorithm, we can greatly reduce these guesses. For binary search to work, we need these start array to be sorted alphabetically.
Using this formula:
$$ \text{Maximum number of guesses} = \log_{2}(n) $$
where n = 2,539,913
$$ \text{Maximum number of guessess} \approx 22 $$
So, using binary search, the number of guesses are reduced to merely 22, to reach the desired name of the star.
Describing Binary Search
When describing a computer algorithm to a fellow human, an incomplete description is often good enough. While describing a recipe, some details are intentionally left out, considering the reader/listener knows that anyway. For example, for a cake recipe, we don’t need to tell how to open a refrigerator to get ingredients out, or how to crack an egg. People might know to fill in the missing pieces, but the computer doesn’t. That’s why while giving instructions, we need to tell everything.
You need to provide answers to the following questions while writing an algorithm for a computer:
- Inputs of the problem?
- The outputs?
- What variables to create?
- Intermediary steps to reach the output?
- For repeated instructions, how to make use of loops?
Here is the step-by-step guide of using binary search to play the guessing game:
- Let
min= 1 andmax= n. - Guess the avg of
maxandmin, rounded it, so that it’s an integer. - If your guess is right, stop.
- If the guess is too low, set
minto be one larger than the guess. - If the guess was too high, set
maxto be one smaller than the guess. - Repeat the step-2.
Implementing binary search of an array
JavaScript and many other programming languages, already provide a way to find out if a given element is in the array or not. But to understand the logic behind it, we need to implement it ourselves.
var primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97];Let’s suppose we want to know if 67 is a prime number or not. If 67 is in the array, then it’s a prime.
We might also want to know how many primes are smaller than 67, we can do this by finding its index (position) in the array.
The position of an element in an array is known as its index.
Using binary search, $\text min = 2 , max = 97, guess = 41$
As $[ 41 < 67 ]$ so the elements less 41 would be discarded, and now
The next guess would be:
The binary search algorithm will stop here, as it has reached correct integer.
The binary search took only 2 guesses instead of 19 for linear search, to reach the right answer.
Pseudocode
Here’s the pseudocode for binary search, modified for searching in an array. The inputs are the array, which we call array; the number n of elements in array; and target, the number being searched for. The output is the index in array of target:
- Let
min = 0andmax = n-1. - Compute
guessas the average ofmaxandmin, rounded down (so that it is an integer). - If
array[guess]equalstarget, then stop. You found it! Returnguess. - If the guess was too low, that is,
array[guess] < target, then setmin = guess + 1. - Otherwise, the guess was too high. Set
max = guess - 1. - Go back to step 2.
Implementing Pseudocode
To turn pseudocode intro a program, we should create a function, as we’re writing a code that accepts an input and returns an output, and we want that code to be reusable for different inputs.
Then let’s go into the body of the function, and decide how to implement that. Step-6 says go back to step-2. That sound like a loop. Both for and while loops can be used here. But due to non-sequential guessing of the indexes, while loop will be more suitable.
- Let
min = 0andmax = n-1. - If
max < min, then stop:targetis not present inarray. Return-1. - Compute
guessas the average ofmaxandmin, rounded down (so that it is an integer). - If
array[guess]equalstarget, then stop. You found it! Returnguess. - If the guess was too low, that is,
array[guess] < target, then setmin = guess + 1. - Otherwise, the guess was too high. Set
max = guess - 1. - Go back to step-2.
Challenge
Implementing binary search...
(If you don’t know JavaScript, you can skip the code challenges, or you can do the Intro to JS course and come back to them.)
Complete the doSearch function so that it implements a binary search, following the pseudo-code below (this pseudo-code was described in the previous article):
- Let min = 0 and max = n-1.
- If max < min, then stop: target is not present in array. Return -1.
- Compute guess as the average of max and min, rounded down (so that it is an integer).
- If array[guess] equals target, then stop. You found it! Return guess.
- If the guess was too low, that is, array[guess] < target, then set min = guess + 1.
- Otherwise, the guess was too high. Set max = guess - 1.
- Go back to step 2.
Once implemented, uncomment the Program.assertEqual() statement at the bottom to verify that the test assertion passes.
TBD
Running time of binary search
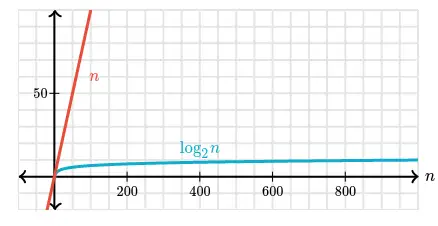
Linear search on an array of n elements might have to make as many as n guesses. We know, binary search need a lot less guesses. We also learned that as the length of an array increases, the efficiency of binary search goes up.
The idea is, when binary search makes an incorrect guess, number of reasonable guess left, are at least cut half. Binary search halves the size of the reasonable portion upon every incorrect guess.
Every time we double the size of an array, we require at most one more guess.
Let’s look at the general case of an array of length n, We can express the number of guesses, in the worst case, as “the number of time we can repeatedly halve, starting at n, until we get the value 1, plus one.” But this is inconvenient to write out.
Luckily, there’s a mathematical function that means the same thing as the base-2 logarithm of n. That’s the most often written as $\log_{2}(n)$.
| n | $\log_{2}(n)$ |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
| 512 | 9 |
| 1024 | 10 |
| 1,048,576 | 20 |
| 2,097,152 | 21 |
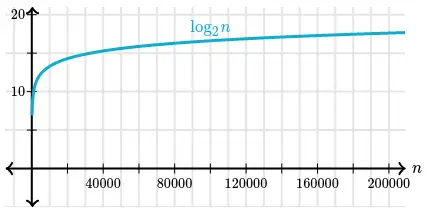
Graph of the same table:
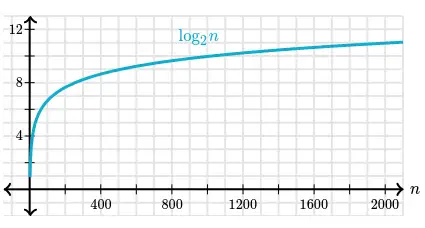
Zooming in on smaller values of n:
The logarithm function grows very slowly. Logarithms are the inverse of exponentials, which grow very rapidly, so that if $\log_{2}(n) = x$, then $\ n = 2^{x}$. For example, $\ log_2 128 = 7$, we know that $\ 2^7 = 128$.
That makes it easy to calculate the runtime of a binary search algorithm on an $n$ that’s exactly a power of $2$. If $n$ is $128$, binary search will require at most $8 (log_2 128 + 1)$ guesses.
What if $n$ isn’t a power of $2$? In that case, we can look at the closest lower power of $2$. For an array whose length is 1000, the closest lower power of $2$ is $512$, which equals $2^9$. We can thus estimate that $log_2 1000$ is a number greater than $9$ and less than $10$, or use a calculator to see that its about $9.97$. Adding one to that yields about $10.97$. In the case of a decimal number, we round down to find the actual number of guesses. Therefore, for a 1000-element array, binary search would require at most 10 guesses.
For the Tycho-2 star catalog with 2,539,913 stars, the closest lower power of 2 is $2^{21}$ (which is 2,097,152), so we would need at most 22 guesses. Much better than linear search!
Compare $n$ vs $log_{2} {n}$ below: